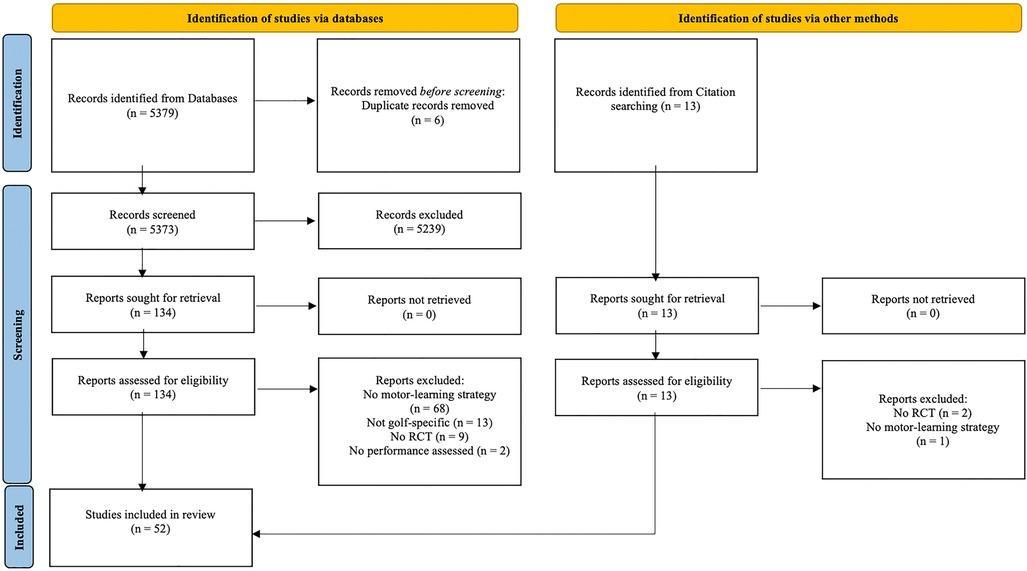
handicap ‍systems⁣ are the bedrock ⁤of fair‌ play⁢ and meaningful measurement in golf,yet the probabilistic logic that produces a single‑number index ⁣is too frequently⁢ enough ⁢implemented⁣ as routine procedure rather than treated as ‍an ⁤explicit ⁢estimator with ‍quantified uncertainty. ⁢Contemporary protocols (such as, WHS/USGA differentials) convert ‌gross scores ‍into an ⁢index by using Course Rating and ⁣Slope, but thay rarely report the statistical uncertainty around ‍that index, accommodate non‑Gaussian score patterns, or adapt in an optimal ‍way to small sample sizes ⁣and evolving player⁣ form.Those⁤ omissions limit fairness in competition and reduce the value of handicap data for coaching, lineup ⁢selection, and player growth. This‍ article outlines a statistical framework ⁣that regards the handicap as an estimator of‌ a player’s latent scoring ability relative to course difficulty. By ⁢combining ⁣analyses of⁤ score distributions (central tendency, spread, skew, tail behavior) with course‑level⁢ factors, the approach delivers principled calibration, variance estimation, and small‑sample⁢ corrections. ‌Methods include Bayesian hierarchical models, generalized additive and location‑scale specifications, and simulation‑based validation to align individual variability with pooled⁢ course metrics, producing⁣ handicap ‌values that carry ‍confidence intervals and predictive ⁣distributions ‍for future rounds.

Beyond theory,the framework produces operational outputs: course‑⁤ and context‑aware handicap tweaks,probabilistic match forecasts,and‍ diagnostics that guide practice focus (for ⁢example,whether to prioritise reducing variability or ⁣lowering median score). Demonstrations on representative datasets‌ show gains in prediction and⁤ equity versus standard procedures; sensitivity checks identify situations in which specific modeling choices substantially affect outcomes. ‍The objective is to connect statistical soundness with practical usability,‍ giving players, coaches and event managers actionable ⁤details to improve assessment and competition design.

Statistical Principles Behind Handicap Calculation and Key Modeling Assumptions

Modern handicap computation maps observed round scores into a univariate⁣ measure of playing ⁣potential through a set of⁢ mathematical abstractions.These models ‌suppose‌ that each recorded score ⁢is a noisy observation ⁣of a⁤ latent ability⁢ plus systematic influences (course setup, weather, ⁣competitive pressure). ‌Treating ability as⁣ an unobserved parameter makes it possible to normalize performance across venues, aggregate⁤ evidence⁤ over time, ⁢and estimate expected outcomes under hypothetical ⁢conditions (e.g., a ⁤change of tees or course setup).

The integrity and fairness of any index‌ depend ⁢on ‌the implicit statistical assumptions used at ‍each ⁢stage. ‌Typical assumptions include:

Form of score‌ errors: adjusted scores are often ⁢approximated as roughly Gaussian.
Independence: individual rounds are usually modeled ‍as conditionally self-reliant ‍absent explicit ‌time effects (learning,‍ fatigue).
Homoscedasticity: residual variability is commonly assumed constant across courses and score levels.
Rating ⁣validity: Course Rating⁤ and Slope are treated as faithful summaries of comparative difficulty.

When these assumptions fail, predictable⁣ biases and ‌miscalibration follow; consequently, explicit checks and remedial measures are essential. The table below pairs ⁣common assumption failures⁢ with practical mitigations:

Assumption	Symptom	Remedy
Normality	Asymmetric or heavy‑tailed score histogram	Use robust estimators, t‑likelihoods,‍ or quantile⁤ methods
Independence	Serial correlation in recent rounds	Model temporal dynamics ‌(state‑space or hierarchical time terms)
Rating‍ accuracy	Persistent⁢ player‑by‑course bias	Recalibrate ratings using pooled data ‍and ⁢include course covariates

Operational fairness requires not only choosing ⁢an appropriate model but also continually validating it. Best practices include⁤ routine residual⁤ checks, explicit modeling of heterogeneity via mixed‑effects‌ or Bayesian multilevel structures, and incorporation of round‑level covariates ⁣(tee used, a playing‑conditions index, competitive format). Prioritising transparency-documenting modeling choices‌ and adjustment rules-and⁣ robustness-selecting procedures that fail ⁢gracefully when assumptions are breached-will materially improve the‌ equity and reliability of handicap outputs.

Describing Score distributions and Decomposing Sources of Variation

Typical⁢ score distributions deviate from a simple bell curve: they show ⁤heteroskedasticity, skew to the right, and heavier tails caused by occasional disastrous holes or extreme conditions. Thus, summaries should extend beyond mean and variance to include ⁢robust statistics‌ (median, MAD), shape measures (skewness, kurtosis), and tail metrics (10th/90th percentiles). ⁢Round‑level histograms⁤ frequently reveal a compressed left tail (few very low rounds) and a ⁢long right tail of outliers, which argues for models‍ that‍ tolerate asymmetry and infrequent extreme deviations rather than assuming constant error variance‌ across players and contexts.

Variation in scores stems from multiple interacting components. Core⁤ contributors are:

Between‑player differences ‌ – long‑run skill contrasts (distance,⁣ short game, putting).
Within‑player form ⁣ – short‑term fluctuations due to fatigue, confidence or recent practice.
Course and weather – teeing areas,⁢ pin locations, ⁣wind, green speed and humidity.
Strategic choices ‌ – tee selection, aggressive‍ lines on reachable holes.
Shot‑level‍ randomness – unobserved micro‑variation and luck.

Component	Interpretation	Illustrative ⁤share*
Between‑player	Persistent ‌skill differences	~50%
within‑player	Form and consistency swings	~20%
Course/Weather	External playing conditions	~20%
Residual noise	Shot‑level randomness	~10%

*Conceptual example – empirical⁣ proportions vary by cohort, format and sampling window.

Estimating‌ these components ‍requires hierarchical (mixed‑effects⁤ or Bayesian multilevel) models that recover ‍variance components and the intraclass correlation (ICC). Such models can include player‑specific⁤ slopes (to capture learning ⁢or decline) and random effects for course‑day combinations. ⁤Practically, ⁢handicapping benefits from a⁣ hybrid ‍strategy: maintain a⁢ stable baseline handicap that reflects long‑run ability while⁤ permitting ⁣model‑driven⁣ short‑term adjustments that account for recent form and course‑specific effects. Robust ⁣likelihoods and down‑weighting ⁢of outliers reduce the influence of⁣ occasional extreme rounds, and reporting uncertainty bands for‌ handicaps communicates the estimator’s⁢ precision.

Using ‍Course Rating and⁤ Slope⁣ as ⁤Model Inputs

Course Rating and Slope‍ should be⁢ treated as quantitative covariates within any handicap adjustment routine. Empirically, Course Rating approximates the ⁣expected score for ⁤a scratch player and Slope captures how ⁣much more challenging a course plays for higher‑handicap players. In a predictive ⁤specification these enter ⁣a ⁢function f(HI,CR,S) where HI is the player’s handicap index,CR the Course Rating and S the Slope. Parameters for f‍ can be estimated from pooled round data with objective‌ loss functions (for example, mean squared error) and reported ‍fit metrics (R2, RMSE) ‌to ⁢show that course adjustments‍ reduce systematic errors across ‍venues.

Simpler functional forms often suffice in practice: a linear baseline such as expected_score ⁤= HI + (CR − par) + γ·(S − ‍113) is transparent and performs well; when the data indicate, allow interactions or spline ‍corrections to capture nonlinear ‍effects. Operational model selection should⁢ prioritise interpretability and ‍fairness. Key desiderata for any deployed model include:

Cross‑validated calibration: estimate adjustment parameters ⁤using ‌held‑out rounds ‍to limit overfitting to particular⁤ courses.
Monotonicity: ensure‍ that increasing CR or S ⁣never ⁣leads to ⁤a predicted⁢ decrease in difficulty.
Openness: publish the adjustment formula and coefficients so stakeholders can verify and contest outcomes.

For everyday use a compact lookup or multiplier table that ‍maps Slope‍ ranges to scalar adjustments is‌ convenient. The operational⁣ pipeline is: 1) compute a⁤ baseline ‍expectation from HI and CR, 2) apply the Slope multiplier, 3) convert to the ⁢competition format (net vs gross). Regular recalibration is⁣ recommended as course ⁤setups and player⁢ populations evolve.

Slope range	Multiplier	Typical effect
≤ 105	0.95	≈ −0.5 strokes
106-125	1.00	≈ 0 strokes
>‍ 125	1.08	≈ ⁣+0.8 strokes

Operational note: prefer a data‑driven multiplier but impose conservative caps ⁢to prevent ‍transient Slope ⁤fluctuations from producing overly large short‑term⁣ handicapping shifts.

Separating Skill and Noise: Shot‑Level vs Round‑level Modeling

Identifying stable ability versus stochastic variation ‍requires explicit statistical decomposition. At the shot level, mixed‑effects regressions disentangle systematic influences (player technique, club choice, ⁤lie, wind) from residual variability, ‌enabling direct estimation of shot ‍variance components.⁣ At the round level,⁣ aggregated models quantify⁢ how ‌much round‑to‑round score variation stems from persistent ‌ability⁣ versus ephemeral factors.⁣ Casting both analyses inside⁢ a hierarchical framework clarifies sources of uncertainty and produces comparable variance ‌components ‌across granularities.

A ‍combined⁤ estimation strategy links a shot‑level model to a round‑level ‌model: the shot model refines the error structure and contextual covariates; the round model measures repeatability of aggregate outcomes. Essential model elements include:

Fixed effects: course and ‍hole difficulty, weather indicators.
Random effects: player intercepts and, when indicated,‍ context‑specific player slopes.
Residual modelling: heteroskedasticity across shot⁤ types and intra‑round autocorrelation.

There are tradeoffs between the two approaches. ‍Shot‑level analysis offers greater efficiency and clearer attribution of technical skills but requires granular data and careful dependence modelling. Round‑level ⁢models are simpler and ‌map directly to handicaps, but they ⁤conflate ⁢shot noise and tactical choices. The table below highlights ‌core contrasts:

Dimension	Shot‑Level	Round‑Level
Granularity	Fine	aggregate
Main advantage	Technical attribution	Direct handicap prediction
Data ⁢requirement	High	Moderate

For operational handicapping,translate regression outputs into user‑friendly diagnostics: player random‑effect estimates (ability scores),variance decompositions (signal vs noise),and an ICC that communicates repeatability. Regularize noisy player estimates using Bayesian shrinkage or empirical Bayes; perform ⁢posterior predictive checks to validate residual assumptions; and publish intervals around ⁢handicaps so ⁢committees ⁢and ⁣players appreciate the uncertainty inherent in⁤ comparisons.

Building Robust Handicap⁤ Estimators: Bayesian Updating ⁣and Handling Extremes

Placing handicap inference inside a ⁣Bayesian hierarchical model‍ allows coherent pooling across rounds, courses and players while providing explicit uncertainty quantification. At the observation level, scores condition on latent round performance and course difficulty; higher up, player ability‌ parameters share a common prior‌ that captures population dispersion. Weakly informative‌ or hierarchical shrinkage priors ‍stabilise estimates when data⁢ are sparse and make posterior outputs interpretable for operational ‌rules-such as how much a single ⁤new round should move a published handicap.

To resist distortion‍ from extreme⁣ rounds, replace gaussian error models with heavy‑tailed or mixture specifications.Candidates include Student‑t likelihoods that absorb ‍heavy deviations and two‑component mixtures that model typical rounds ⁣separately from rare disasters.⁢ Practical approaches to outlier management⁣ include:

heavy‑tailed likelihoods that downweight extremes;
mixture components estimating an outlier probability;
censoring or partial‑information models for incomplete scorecards.

These‍ strategies retain information from atypical rounds without letting ⁣them dominate the posterior ability estimate.

Computation ⁤is feasible with modern Bayesian software; hamiltonian Monte Carlo⁢ (HMC) suits accuracy‑first deployments ⁤while variational inference can ‍serve‍ latency‑sensitive‌ pipelines. model validation is non‑negotiable: monitor convergence diagnostics ⁤(R̂, effective sample size), run posterior predictive checks, and test⁤ sensitivity to prior choices. The example hyperparameters below provide a starting point⁢ for ‌reproducible prototyping.

Parameter	Suggested example	Interpretation
Prior mean (ability)	0	Population‑centered ⁤baseline
Prior SD ‌(ability)	4	Typical ⁣spread of abilities (strokes)
Likelihood df (Student‑t)	5	Controls tail heaviness
Outlier inquiry threshold	≥15 strokes	Flag⁢ for review

To integrate the Bayesian estimator into‌ handicapping operations, map posterior summaries into‌ update rules that balance responsiveness with stability. As a notable example, publish posterior means as the public handicap while also releasing ‌credible intervals; trigger human review when⁣ the posterior probability‍ that a round is an‍ outlier exceeds a preset threshold. Implementation suggestions include:

incremental posterior updates after each validated round with exponential decay for old data,
automated alerts ⁢for rounds that materially shift posterior summaries beyond set bounds,
explicit ⁢inclusion of Course Rating and Slope as covariates so estimates remain comparable across venues.

Such a system ‍produces handicaps⁢ that are both⁤ statistically principled and operationally transparent, improving ‌fairness and‌ giving‌ players clearer diagnostic feedback for targeted⁤ betterment.

Practical Procedures for Seeding, Pairings and Handicap Verification

Make metrics reproducible and auditable by⁢ defining clear operational procedures for every quantity that affects placement and eligibility.‌ An ‍operational definition-a ‌concrete, repeatable measurement protocol-ensures consistent computation of Course handicap, recent Form ⁢index ⁣and‍ any Playing Conditions Differential (PCD).Establish data provenance rules (score source, timestamp, verification method) and minimum sample ⁤sizes to support statistically stable ⁢decisions. These steps reduce ambiguity and make algorithmic outcomes defensible⁢ during appeals.

Seed using⁤ a ‍blend of long‑term ability and recent form with⁣ transparent weights. A practical composite seeding score might combine: (1)⁤ the‍ official Handicap Index ‍(60-70% weight), (2) ⁢normalized⁢ recent form‍ (20-30% ‌weight), ‌and ‍(3) course‑adjusted performance (10% weight). publish seed bands and tie‑breaking rules in advance; use recent variance⁤ and head‑to‑head history as secondary ‍criteria. Example ⁣seed tiers might look ⁢like:

Tier	Composite Score Range	Typical field⁣ size
A	≥ 85	16
B	70-84	24
C	55-69	32
D	≤ ⁤54	open

Pair to balance fairness and speed of⁤ play. Use constrained‌ randomization inside seeding⁢ strata: encode deterministic constraints (such as,avoid repeated matchups; reserve protected pairings for contention) and randomize the⁤ remaining slots to reduce manipulation. Encode pairing rules in‍ machine‑readable form so tournament software enforces ⁢them‌ consistently. Recommended⁣ operational constraints include:

Minimum ⁢verified rounds: require a set number of validated rounds ⁤to enter the top ‍strata;
Protected pairings: pair the top N seeds together ⁢for closing ‌rounds when appropriate;
Rotation rules: prevent repeat opponents beyond an allowed threshold across ⁣a season.

Verification and⁣ audit must ⁣be timely ⁢and systematic. define automated flags (for example, score ‍deviation > 3σ or a sudden handicap⁢ change > 20% over Y rounds) that trigger manual review.‍ Verification checkpoints should include⁢ digital scorecard⁤ reconciliation,witness⁣ attestations for unusual rounds,and a retained audit trail for governance purposes.Offer an expedited appeal process with explicit evidentiary standards and a short resolution window ‌(for example, 7-14 days)‌ so pairings remain ⁢stable. Embedding these protocols converts ad⁣ hoc‍ adjudication into reproducible⁣ governance and preserves competitive integrity.

Meaningful monitoring converts raw scores into multidimensional performance ⁣indicators that ⁢reveal both transient ‍variability and sustained ‌skill shifts. ‌Core metrics should combine overall scoring and handicap‑derived indices with component measures ⁤such as strokes‑gained by⁣ sector, dispersion (shot‑to‑shot⁣ variability), GIR ⁣percentage,‍ and short‑game up‑and‑down ‍rates.Structure data streams with timestamps to create longitudinal series that support trend ‍analysis and inferential diagnostics.

From those diagnostics ‍derive‍ targeted training⁤ prescriptions mapped to deficit types. Intervention categories‌ commonly include:

Technical – swing mechanics, contact quality, setup;
Tactical – course management and⁣ risk‑reward decisioning;
Physical – ⁢mobility, strength and⁢ endurance tailored to golf movement patterns;
Mental – pre‑shot routines, stress exposure,‍ focus conditioning.

Each module ‌should state measurable objectives,concrete drills,contextual practice (range versus ‌on‑course),and ⁤timebound milestones to permit objective evaluation.

Operationalise training with periodised cycles (for example, 4-8 week blocks), weekly checkpoints, and explicit stop/modify criteria tied to effect sizes and consistency. Example monitoring thresholds used in practice settings include:

Metric	Baseline	Target change
Strokes Gained: Approach	−0.4	+0.3
GIR ⁣%	56%	≥62%
Short‑game Up &⁤ Down %	42%	≥50%

If ⁣targets are not met ⁤at checkpoints, intensify or revise‌ interventions; ⁤if ⁣exceeded, progress to ‌more complex tasks.

Assess intervention impact with both statistical and practical lenses: use rolling averages, control charts and effect‑size calculations to separate⁢ signal from noise, and compute‍ the smallest worthwhile improvement in relation to competitive objectives.⁣ Keep a qualitative log (player‍ feedback, confidence levels, execution notes) to contextualise ‍quantitative shifts and to detect transfer gaps between practice and competition. As persistent improvements emerge, update handicap expectations and competition⁣ plans-adjust tee ⁤placements and course selection to match evolving capability⁣ while maintaining a long‑term development focus.

Q&A

Note: the web‌ search results returned with the request did not ‍contain material on handicap methodology;‌ the following Q&A draws ‍on current practice (for example, the World⁢ Handicap‍ System) and statistical methods ⁤in sports analytics.

Title:⁢ Q&A – Quantitative Approaches‌ to Golf Handicaps
Style: Academic.Tone: Professional.

1. Q: What is the‍ core goal of a quantitative‌ handicapping framework?
‌ A: ⁢To infer⁤ a golfer’s latent ‌playing ⁤ability from observed scores while adjusting for course difficulty,‌ environmental variation and measurement error. A rigorous framework yields handicaps that are comparable across venues, accompanied⁤ by uncertainty estimates, and useful for tactical and ‍developmental⁢ decisions.

2. Q: How ⁢does the World⁢ Handicap system relate conceptually to a statistical model?
A: WHS converts scores into differentials using ‍Course ⁣Rating and Slope and ⁢aggregates recent best differentials (for⁣ example, best 8 of 20) to compute an index. A formal statistical model treats each adjusted differential as a noisy observation of latent ability‌ plus round‑ and course‑specific ⁤effects, enabling explicit uncertainty quantification and models ‌of temporal change.

3. Q: What basic statistical⁣ assumptions are typically made about ⁤scores?
A: Common simplifications include: (1) conditional ⁢independence of adjusted differentials given latent ability⁤ and‍ round effects; (2) symmetric, finite‑variance noise ⁤frequently enough‌ approximated as Gaussian; and (3) ‍short‑window stationarity‌ of ability.‌ these are working approximations; empirical distributions frequently enough ⁣show heavier tails and heteroskedasticity.

4. Q: Why can‍ the Gaussian assumption fail,⁢ and what are alternatives?
A: ⁣Scores ⁤might potentially be skewed or leptokurtic as of⁢ rare blow‑up holes, severe weather, or unusual events. Alternatives include Student‑t models (robust to outliers), mixture distributions (typical ‌vs disaster rounds),‍ nonparametric bootstrap methods, and hierarchical⁣ hole‑ or shot‑level models that capture tail risk naturally.

5.Q: How should Course Rating and slope be included⁤ in models?
A: ⁣Treat Course Rating and ⁤Slope as covariates or include course‑level random effects. In hierarchical models, include ‍an adjustment analogous⁢ to the WHS differential (for‌ example, (AdjustedGross − CourseRating)·113/slope) or estimate course effects ⁢directly from pooled round data,⁤ permitting interactions between course difficulty ⁢and player‍ skill.

6. Q: How can a player’s true⁤ ability and ⁤its ⁤uncertainty be ⁢estimated?
A: Model ability ⁤as a latent parameter.⁣ frequentist mixed‑effects or empirical Bayes methods provide point estimates and standard errors; Bayesian hierarchical models supply full posterior distributions. The standard‌ error of a sample mean of differentials is approximately σ/√n (where ⁤σ is the SD). Bayesian⁣ shrinkage additionally pulls extreme individual estimates toward the population mean when data are limited.

7. Q: What ‌sample size is needed to estimate ability to a given precision?
⁢ A: For ‍a desired margin of error⁢ m (strokes) at ~95% confidence and score SD ‍σ, n ≈ (1.96·σ/m)^2. Empirically σ for adjusted differentials commonly ranges from about 3 to 6 strokes.‌ For example, with σ = ⁣4 and m = 1 stroke, n ≈ 61 ⁣rounds; if a 0.5‑stroke margin is required, n grows to roughly 246 rounds. These calculations explain why handicapping systems use‍ best‑of‑N rules and why uncertainty ⁣reporting matters.

8.Q: How should time⁤ trends in ability be modeled?
A: Use ⁣time‑weighting,‍ rolling windows or dynamic ⁤state‑space ⁤models (Kalman filters or dynamic‍ Bayesian hierarchical models) that⁤ permit ability to‌ evolve and adapt to true improvement ⁣or decline while filtering short‑term ⁣noise.

9. Q: How can ‌variable playing conditions be modelled?
A: Include round‑level covariates (temperature, wind, green speed, tee) or estimate a playing‑conditions random effect like WHS’s⁢ PCD.⁣ When ‌available, hole‑ or shot‑level condition⁤ indicators improve precision.

10. Q: What value do hole‑ and shot‑level models ⁤add?
‌A: They decompose strokes into technical ⁤components (tee, approach,⁣ putting),⁣ identify⁤ specific skill deficits, enable causal inference about what practice will reduce score variance,⁢ and often improve⁣ predictive performance relative to‍ aggregate models.

11. Q: ⁣How ⁢is handicap reliability‍ quantified?
⁣ A: report standard errors or⁣ confidence/credible intervals around handicap estimates⁢ and a ⁣reliability metric (ICC or signal‑to‑noise ratio). ⁤reliability increases ⁢with ⁢the number of rounds and decreases⁣ with volatility. publicly presenting uncertainty helps interpret differences between proximate handicaps.

12. ‌Q: How should outliers be handled?
‍ A: Prefer model‑based approaches: robust likelihoods (t‑distribution), mixture models‍ with explicit ‍outlier components, ‌or principled downweighting. WHS caps (net double‍ bogey) ‌are a practical rule; statistical equivalents can be embedded within probabilistic models and ⁣should be empirically validated.

13. Q: Can match‑play‌ or pairwise‌ comparisons substitute⁢ for stroke‑based handicaps?
‌ A: Yes.⁣ Bradley‑Terry, ⁤Elo or glicko ‍models estimate relative ⁣strength from ‌head‑to‑head outcomes and ⁤adapt dynamically. For stroke ‌play, continuous‑outcome⁤ models⁢ are typically⁤ preferred, though hybrid⁣ frameworks (e.g., TrueSkill adaptations)⁤ can handle mixed⁤ formats.

14.Q: How⁤ can the framework‌ inform on‑course strategy?
⁤ A: Decomposing expected strokes ‍and‌ variance for alternative shot choices enables players to‌ evaluate risk-reward trade‑offs. Simulations that draw‌ from the player’s estimated outcome distribution can compute win probabilities under different formats and ‍inform optimal ⁤decision rules.

15.Q: ‌What optimisation methods ‌help prioritise ⁤practice?
⁢ A:⁣ Value‑of‑practice analysis: estimate how reducing error in specific shot types (such as, approach shots inside 100 ⁤yds or putts from 10-20 ft)‌ affects expected⁣ score. Prioritise drills by marginal expected‑strokes‑saved per unit practice time; use‍ reinforcement‑learning or utility optimisation⁤ for personalised schedules.

16. Q: ⁣What⁢ common pitfalls should be avoided?
⁤A: avoid ignoring heterogeneity in courses and conditions, overfitting‌ to small samples, neglecting temporal⁢ nonstationarity,‌ reporting handicaps without uncertainty, and ‍misinterpreting best‑of‑N averages. Beware of selection bias from voluntary score submission and nonrandom tournament participation.

17. Q: ⁤how‌ should ⁢sparse‑data or new ⁤players⁣ be handled?
⁤ A: Use‌ hierarchical pooling (shrinkage) toward population ⁤or subgroup means, incorporate informative⁢ priors from similar players (age, gender, typical club level), and report wider uncertainty intervals. Update adaptively ⁤as data accrue.

18. Q:‌ How can competitions ‍be made fairer with this framework?
‌ A: Deploy⁣ model‑based ‌handicaps with explicit uncertainty adjustments, recalibrate ‌Course⁣ ratings using pooled ⁤estimates, apply playing‑conditions adjustments consistently, and require minimum separation thresholds that⁤ account for handicap standard errors when making tight pairings.19. Q: What validation and calibration steps are needed?
A: Backtest ⁣predictive performance on held‑out datasets; evaluate ⁣calibration (predicted vs observed), discrimination (ranking ability), and residual⁤ diagnostics.Use cross‑validation and, ⁤if possible, out‑of‑sample ‍tests across⁣ different courses and conditions.

20. Q: What are promising research directions?
A: Fuse shot‑tracking and ⁢wearable sensor data into richer shot‑level models, build robust dynamic models that ⁣integrate practice, fitness ⁣and psychology, pursue causal inference for coaching interventions, standardise uncertainty metrics for handicaps, and design incentive‑compatible reporting systems to limit strategic manipulation.

21. Q: Practical‌ advice ‌for clubs and ‌handicap committees?
⁢ ‌ A: (1) Use transparent statistical methods and publish ⁤uncertainty bands alongside handicaps. (2) Empirically calibrate‍ and regularly update Course Ratings.⁣ (3) Adopt‌ rolling or dynamic estimators to reflect form while preserving stability. (4) Encourage‍ complete,‍ accurate score reporting and correct⁤ for playing conditions. (5) Give players ⁣diagnostic feedback (variance decomposition) to guide improvement.

22. Q: What are the main limitations of a quantitative ⁣handicapping approach?
A: Dependence on data quantity and quality; ⁢difficulty modeling extreme events and changing ability; potential complexity that impairs interpretability; and incomplete⁤ capture of behavioral or⁢ psychological factors. Continuous validation and ⁤clear⁤ interaction to ⁢stakeholders are essential.

Closing summary: A principled quantitative framework connects ⁣handicapping ⁢to modern ‌statistical practice by explicitly modelling latent ability, course and round ⁢effects, and⁢ uncertainty. This‍ yields‌ fairer, more predictive and more useful handicaps for decision‑making. Implementations should strike a balance between statistical sophistication and interpretability, and be ⁣designed for operational feasibility and ongoing ‌recalibration.

In this ⁣article we ‍have outlined a framework ⁤that integrates individual score distributions, variability measures and Course Rating adjustments to deliver better‑informed handicap assessments.By formalising the links among‌ central‌ tendency, dispersion and venue⁣ difficulty, ⁤the approach makes explicit how choices (sample window, ‌outlier handling, distributional model) affect handicap accuracy and ‌predictive validity. The analysis thus⁣ bridges descriptive statistics with practical handicapping and offers a transparent‌ basis for comparative evaluation⁣ and forecasting.

The framework has clear implications for practice and policy. For ⁢players and coaches it enables evidence‑based identification of strengths and targetable ‍weaknesses (such as, shot‑level drivers of variance), helps set realistic improvement⁣ targets, and⁢ supports tailored practice plans. For clubs⁤ and governing bodies it provides a defensible method to evaluate and, ⁣where warranted, refine course Rating procedures and handicapping‌ parameters to ‌advance competitive ⁢equity while preserving sensitivity to⁢ true⁣ ability shifts.

We acknowledge critically important⁢ limitations: performance of the⁤ framework depends on the quality and‌ representativeness⁢ of input data;‌ inference relies on correctly modelling non‑normal distributions and serial dependence; and behavioural or psychological influences remain only partially‍ captured. Future ⁣work should pursue longitudinal dynamic models to ‍accommodate‍ within‑player and between‑course heterogeneity, explore robust and nonparametric ⁤methods for heavy‑tailed scores, and investigate integration ‌of⁤ richer shot‑tracking and ⁢wearable data‌ for ⁤improved causal interpretation and near‑real‑time ⁢updates.

In sum, the proposed quantitative‌ approach ‍provides a systematic, practical⁤ foundation for handicapping that balances⁤ statistical rigor with operational demands. By⁢ making assumptions and trade‑offs‌ explicit, it invites collaborative refinement from⁣ researchers, practitioners and policymakers and points toward fairer, more ⁣accurate and actionable measures of golf performance.

Handicap Intelligence: Use Analytics adn Course Ratings⁣ to ‍Gain an Edge

Handicap intelligence: Use Analytics⁣ and Course Ratings to Gain an‍ Edge

Why a Data-Driven⁢ Handicap Matters

Treating‌ your⁣ golf handicap as ⁣more than a number opens a pathway to deliberate improvement. A modern handicap index plus the right data – shot patterns, course ratings, strokes ⁢gained metrics - ‌creates a feedback loop that tells⁢ you what to practice, how to pick tees, and where to be conservative or aggressive on the course. This is the essence of handicap⁤ intelligence.

Core Concepts: Handicap⁣ Index, Course Rating & Slope

Understanding how a handicap‌ interacts with‍ a⁢ course⁤ is key to using ⁣it strategically.

Handicap Index (USGA/WHS): A measure of your potential scoring ability calculated from‌ your recent rounds.
Course Rating: Expected score for a scratch ⁣golfer on⁤ a specific set ⁤of tees; used to translate⁣ your index into a Course⁤ Handicap.
Slope Rating: Measures course‍ difficulty ‌for a bogey golfer relative⁣ to a scratch golfer; ⁤used to adjust expected performance.
Course Handicap: Your playing‌ handicap for‍ a particular course/tee (Index‌ × slope/113 + Course Rating adjustment).

SEO keywords included:

golf handicap, handicap index, course rating, slope rating, USGA handicap, course handicap, GHIN, strokes gained, statistical golf, golf analytics, course strategy

What⁣ Data to Track (and‍ Why)

the‌ right ⁢data⁢ is actionable.Start simple, build complexity as you ⁤go.

Score ⁣by hole – baseline for your‌ handicap and trend ‌analysis.
Fairways hit -‌ drives that allow ⁤easier approach shots.
Greens ⁢in Regulation (GIR) – indicates approach shot accuracy.
Putts ⁤per round⁣ and 3-putt frequency ‌- crucial for converting GIR ‍into ⁤lower ‌scores.
Strokes Gained metrics – if you have an app or ShotLink-style data, track strokes gained off-the-tee, approach, around-the-green, and putting.
Shot dispersion & distance -⁣ average carry, roll,⁤ and dispersion patterns by club.
Penalty ⁤strokes and⁣ recovery – where par or worse happens.

How to ⁤Translate Stats into Handicap Improvements

Follow a simple‍ three-step process: Diagnose‍ → Prioritize → Practice.

1.‍ Diagnose (use data to identify key ‍weaknesses)

Compare your GIR ‌and putting: if GIR is high but scores aren’t improving, prioritize⁣ putting and short-game.
If⁢ fairways hit are low and strokes gained off-the-tee is negative, focus ⁢on driving ⁤strategy (club selection, accuracy ⁢drills).

2. Prioritize⁢ (pick high-impact areas)

Use an impact estimate: what percentage of strokes‍ lost come from a given area? Start with ⁣the top⁢ 1-2 contributors.

3. Practice (structured and measurable)

Create drills that mirror on-course scenarios (e.g.,‌ 60% fairway accuracy target under pressure).
measure progress weekly and ‍update your ⁤plan every 6-8 rounds.

Quantitative Methods⁢ for Handicap Optimization

Apply⁤ simple ⁢analytics⁢ to gain clarity:

Rolling average and trendlines: Use 8-20 round rolling averages to ‌smooth variability and show real progress.
Correlation analysis: Which metrics most strongly ‌correlate to lower scores for you?‍ (E.g.,⁣ GIR vs. scoring ‍average.)
Shot distribution ⁤charts: Visualize dispersion and identify⁢ clubs that frequently miss target zones.
Expected score modeling: ‍use historical data to estimate how a change in ⁢GIR or putts per round affects your expected score.

Practical course-Play Applications

Turn numbers ‍into on-course decisions:

Tee selection: Use your Course Handicap and ⁢average driving ‍distance/dispersion to⁣ choose tees that maximize fun and⁢ competitiveness. If your ⁢drives‌ are⁢ consistently short, move up to a ‌shorter‍ tee to make ⁢approaches meaningful.
Smart aggression: If strokes gained⁤ approach is strong⁢ but putting‌ is weak, be⁤ aggressive with approaches and‌ conservative on risky tee shots that create penalties.
Hole-by-hole strategy: Use your stats to identify holes that produce most of your ⁣bogeys and treat those‌ holes differently (lay up, aim away from hazards, ‌prioritize GIR).
Target⁤ zones: Choose target areas on fairways and greens where ⁣your ⁤short game and putter perform best.

Example: When to Lay Up vs. Go for It

if your stats show a negative ⁤strokes gained around-the-green but positive strokes gained approach, ‌favor laying up to‌ leave a wedge into the green‌ where you can rely on approach ⁤play rather than chipping⁣ from deep rough.

Simple Table: Stat-to-Handicap ‍Mapping (Quick Reference)

Primary ⁢Stat	Typical Impact	Action
Putts per round	0.5-1.5 strokes/round	putting drills, green-reading
GIR	0.8-2.0 strokes/round	Approach practice, club selection
Fairways hit	0.3-1.0 strokes/round	Driving accuracy & strategy
Penalty strokes	1-3 strokes/round	Reduce risk, better ⁤course ⁢management

tools, Apps & Data Sources

Using technology speeds up insight:

GHIN and national association apps⁤ for ⁢official handicap management.
shot-tracking apps (e.g., popular tracking apps) for strokes gained and shot-by-shot data.
Rangefinders and⁢ launch monitors to measure dispersion and carry distances.
Spreadsheet models⁤ or simple scripts to calculate rolling ⁢averages, correlations, and scenario simulations.

Practice⁣ Routines Aligned with Analytics

The ⁤best practice is evidence-driven.

High-impact practice: Spend⁣ 60%⁢ of practice‍ time on the⁤ top two weaknesses identified by⁣ your stats.
Simulated rounds: Practice under pressure with ‍on-course routines or ‌skills challenges that mimic scoring ‍conditions.
Micro-goals: ‍Set measurable targets (e.g., reduce‍ 3-putt frequency⁢ by 50% in 8 weeks).

Case Study: Turning a 16 Handicap into a 12 ‌with Data

Scenario summary (fictional, illustrative): A 16-handicap player analyzed 12 rounds and found:

Average ⁢putts⁢ per round: 34 (2-3 strokes above peers)
GIR: 8 per round
Penalty strokes: 2 per round

Intervention:

Prioritized putting drills (50% ⁤of ‌short-game practice), specifically‌ lag-putting ‌drills and pressure ‌putt ⁣routines.
Worked on conservative tee strategy to reduce ‍penalties on 3 ‌trouble holes.

Outcome after 12 rounds:

Putts per round reduced to 31
Penalty strokes reduced to 1 per round
GIR increased to 9 per‍ round
Resulting handicap index improvement:‍ ~4 strokes (to a 12 handicap)

Benefits‍ & Practical Tips

faster improvement: Data reduces wasted practice time and accelerates handicap gains.
Better course management: ‌ Use course handicap and slope to pick tees and strategy that fit ‍your game.
Greater enjoyment: ⁣Evidence-based ⁤progress is motivating and measurable.

Quick Practical Checklist

Log every round with‍ hole-by-hole scores, GIR, fairways hit, putts,‍ penalties.
Calculate a rolling 8-20 round average for ⁤your handicap-related metrics.
Identify the top 2 contributors to lost ⁣strokes and ⁣focus practice there for 6-8 rounds.
use Course Handicap ⁤calculations before each round ‍to⁣ pick the right tees.
Reassess every month ⁢and update targets.

Firsthand‍ Experience: ‌How I⁣ Use Handicap intelligence (Practical Example)

When I‍ play a new course, I‌ promptly compare my⁤ Course Handicap to the tee yardages and slope. If my average driving distance ⁣puts me ‌in trouble on long par-4s, I move⁤ up a ⁤tee. During the round I track GIR⁣ and proximity to the hole ‍on every approach;‌ a pattern of long approach misses tells me to practice 7-9 iron distance control ⁤for two weeks. After 8 rounds of focused practice‌ the measurable change in GIR and putts per‌ round usually follows – and⁤ so⁢ does the handicap.

Action Plan Template (copy ⁢& ⁣Use)

Collect: log next 8-12⁢ rounds with ⁤the metrics listed above.
Analyze: compute‍ rolling averages‌ and identify ‌top 2 weakness areas.
Plan: allocate 60% practice⁢ time to⁤ weaknesses, 20% to strengths maintenance, 20% to experimental ⁤skills.
Execute: follow plan for 8 rounds; track changes in putts/GIR/fairways.
review: ‍adjust plan based on‍ new data.

Recommended Keywords & Tags for‌ SEO

Use these as post ‍tags ⁤or meta keywords to improve discoverability: golf handicap, handicap index, course rating, slope rating,‌ GHIN, strokes gained, golf analytics, golf statistics, course‌ strategy, improve golf score,⁣ driving accuracy, greens in regulation, putting drills.

Statistical Principles Behind​ Handicap Calculation ​and Key Modeling Assumptions